1. A problem
Too often, in too many classrooms, students feel that math has no purpose. What they’re learning may be useful for a test, but that’s far off — and not something they choose to take. Doing well on a test helps their grade point average, but that’s even farther off — and again, not something they’ve chosen to take.
The “why” behind learning math is too far in the future, and imposed on them.
What we need is a way to gin up purpose in math that takes agency seriously, and that can scale to every math lesson.
2. Basic plan
Every day in an Egan classroom, the teacher can begin the math lesson with a Boss Question — a single problem that…
requires students to understand more-or-less all the lesson’s content to solve
is harder than anything in the lesson itself
is ridiculous (or captivates interest in some other way)
It’s best if the Boss Question is written down and affixed on a wall. This way students can continue to see it throughout the lesson, and afterwards.
For a few minutes, students are encouraged — but not forced — to try to solve it. One thing they can do is go to the paper, and write down a specific question about it — something they don’t understand.
If they’re able to solve it, they can ignore the teacher’s verbal lesson, and move directly to their book’s practice problems (their would-be homework). If they’re not able to solve it, they’ll start listening to the lesson the teacher gives.
The teacher — caveat emptor — may find it wise to pause during the lesson and give students another few moments to reconsider the Boss Question.
So far, this is all a description of what could be called lesson-sized “Miniboss Questions”. We can also use “Superboss Questions” — sized to fit a whole chapter or unit.
Superboss Questions can be hung up at the beginning of a new chapter in math (usually once every 2 or 3 weeks, though this will differ by curriculum) in a more permanent location. They are, naturally, much harder and weirder looking than the Miniboss Questions. When they’re hung up, students are given a whole class period to walk around, trying them out, talking about them, and (as always) writing down specific questions about the problem:
"what does this symbol mean?"
"how would you find the area of a triangle, if you don't know both the sides?"
"what does 'percent' even mean, anyway?"The goal in all this is to give a context for the lessons themselves — now they’re tools for solving problems that the students have already seen, and have at least some interest in solving.
3. What you might see
Imagine walking into a third-grade classroom on a Wednesday morning at the start of a perfectly ordinary math class. The teacher begins by putting up a copy of the day’s Miniboss Question:
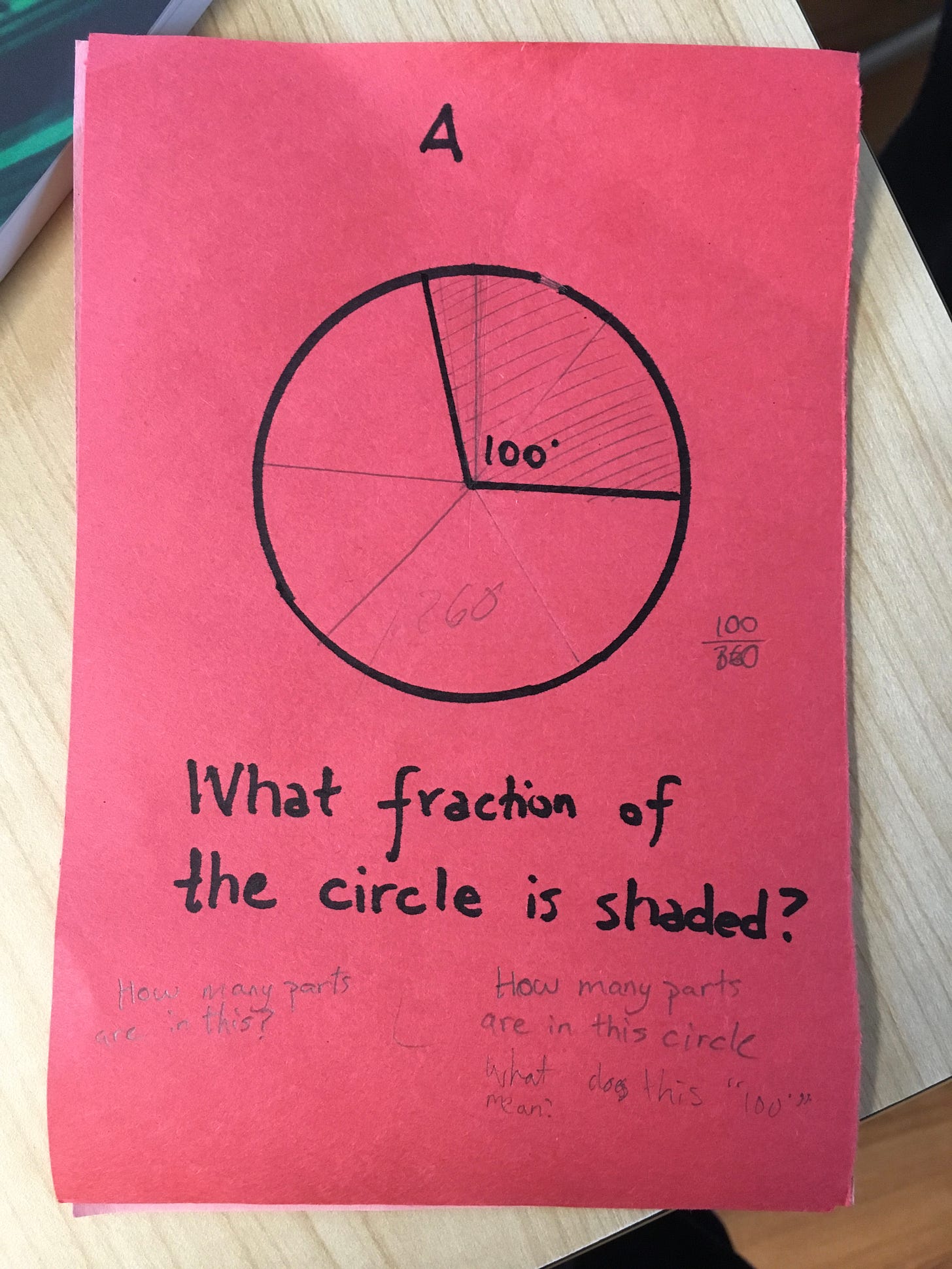
You see eight-year-olds scratching their heads: it feels like the answer should be easy. But how to do it? They talk to each other; when they ask a question of the teacher, the teacher just raises his eyebrows and smiles like the Cheshire Cat. After a few more moments, the lesson commences.
At a random point in the lesson a student’s hand shoots up. He shows the teacher an answer, and the teacher… smiles, and shakes his head: nope. The student scowls, and the lesson continues.
Soon, another student raises her hand, and shows her answer: yep. She begins working on the homework, and the teacher returns to teaching his lesson.
Heck, you’re probably imagining more right now! Commenting on these weekly pattern language posts is a perk for paid subscribers, but you can become one for just $5/month.
4. Why?
Heroic deeds should feel heroic.
Too often, we communicate that math is easy, but we ask more of students in math class than we might realize. As Carlo Rovelli points out in Anaximander and the Birth of Science, we expect the sum of all of Egypt’s, Sumer’s, and Babylon’s mathematics to be mastered by every student by the time they turn 10. (And it only gets harder from there.)1
To honor this, it’s only right to help students feel that they’re accomplishing something as they figure out math.
Starting with Boss Questions frames math as a heroic undertaking.
5. Egan’s insight
Where do we see this in the human experience?
Modern math was sparked by wandering wizards swapping riddles on the road.
No, really: the utter basics of arithmetic and geometry came from Babylonian astrologers, who had spent centuries honing the art of tracking the stars to foretell the future of the state. When Cyrus the Great conquered in 539, Babylon became part of the Persian Empire. Monotheistic Zoroastrianism was in; polytheistic astrology was out. Jobless, astrologers took to the road, finding rich individuals in places like Greece to tell horoscopes to… and swap math riddles with. They couldn’t take the cuneiform tablets with them, but they had scores of mathematical puzzles in their heads. They could tell these, draw these in sand and challenge other travelers with.
Simple questions, designed to be interesting, given as challenges which one could choose to tackle or not — this is how Greeks first fell in love with math.
How might this build different kinds of understanding?
Our weekly reminder: At the heart of Egan’s understanding of education is the notion that, for humans, certain practices and formats of information are special. Egan calls them “tools”, because throughout history, cultures have used them to pass themselves down. He groups them into five “toolkits” — SOMATIC (🤸♀️), MYTHIC (🧙♂️), ROMANTIC (🦹♂️), PHILOSOPHIC (👩🔬), and IRONIC (😏).
Well.
The reason to create problems that aren’t part of the “official” curriculum is to cultivate 🤸♀️ PLAYFULNESS; making the problems nonsensical triggers our 🤸♀️ HUMOR. And while they don’t need to be solved, just offering a small number of problems may secure 🤸♀️ EMOTIONAL ATTACHMENT.
A simple-looking problem is a 🧙♂️ RIDDLE, and provokes a 🧙♂️ SENSE OF MYSTERY: we want to find the answer.
Calling this a challenge (and playing up how we’ve created the hardest problems possible) will be appreciated by students who feel the need to probe the 🦹♂️ EXTREMES and LIMITS of REALITY.
And encouraging students to write down questions and invent stratagems is similar to proposing 👩🔬 HYPOTHESES & 👩🔬 CONDUCTING EXPERIMENTS.
6. This might be especially useful for…
Students who can learn math on their own
Some minds are specially-tuned toward mathematics; the smart thing to do for these kids is to get out of the way. Boss Questions function as a sort of pre-test, allowing kids to skip to the end.
Students who crave independence, but still need lots of help
Boss Questions reframe the lesson as helping students do what they want to do.
Teachers who want to understand their students better
Watching students try to solve a problem before the lesson starts gives the teacher a sense of what the students know, and don’t know — they’ll automatically change the lesson to match what the students understand.
7. How could this go wrong?
A. No one cares about them
No one tries them. They sit, dead, on the wall, while students socialize.
B. Students care about them too much
These become too enjoyable, and the teacher can’t break in with the actual lesson. Teachers can brag about energized learners… but little learning happens.
C. They become obligatory
The Empire strikes back: teachers start using them for grades, or tiger parents start pressuring their kids to do them. The sense of freedom is lost.
8. Classroom setup
How might the physical classroom environment support this?
As Peter Liljedahl (below) points out, there’s something magical about pointing at something on a wall.2 How might we plan for the wall space to do this wonderfully?
One of the things that Montessori and Waldorf schools understand is how amazing a unified aesthetic can feel. This might branch into the artsy-fartsy, but what sort of paper can we get for this? What sorts of writing utensils?
9. Similar stuff (others are doing)
Who’s doing anything similar to this?
Julia Robinson Math Festivals
When I lived in Seattle, I volunteered each year at the local Julia Robinson Math Festival, run by Dan Finkel & Katherine Cook of Math for Love. JRMF’s are non-competitive, well, festivals! Kids poured into a gymnasium scattered with tables manned by experienced math educators armed with simple, progressively more challenging math problems. The beautiful thing: the kids were free to go wherever they wanted.
Thinking Classrooms
Peter Liljedahl3 (who coincidentally — ??? — happens to be at Simon Fraser University) has championed the practice of “Thinking Classrooms”. The gist: usually we assume that “math” means students sitting by themselves staring down at paper. What Liljedahl’s approach assumes is that maybe this… sucks? Replace sitting with standing, isolation with fluid groups, paper with windows (or floor-to-ceiling whiteboards), and staring down with looking up, and suddenly doing math feels alive again.
Dan Meyer
Dan Meyer excels at finding ridiculously interesting math problems in utterly boring aspects of daily life (like slicing cheese or getting ripped off at the gas station). His videos presenting these problems are almost… hypnotic? His is an art that I’d love to bring into our school.
10. Open questions
The terms “question”, “problem”, “puzzle”
I’m using these terms interchangeably. Is there any good reason to not?
Practical ways to make this work with large groups?
Kristin and I made these for ridiculously-small math groups — 3 or 4 students. I have full faith that these can be modified for regular-sized classes… but I don’t know how, yet.
FINAL Boss Questions?
Okay: how far might we push this? I can imagine an Egan classroom putting up really hard problems — years ahead of anything kids can do. GRE problems, Art of Problem Solving problems, problems that are still actually unsolved…
AI math tutors?
Maybe the future of math teaching isn’t large groups at all — maybe AI tutoring really will bring about the long-sought dream of individualized learning a reality.4
Imagine we welcome our new computer overlords and hand them the K–12 math curriculum. No prob: what else could we employ this method for?
11. How could this be done small, now?
If you’d like to make a draft Miniboss Question of a single lesson (or Superboss Question of a unit) and post it in the comments below, I’ll give constructive, kind feedback. The devil’s in the details,5 and working through examples will help us all get a sense for what these things can really look like. Any math curriculum is fine, and at any level.
If anyone would like to make a set of these for a popular curriculum and sell them, I’d be happy to spread word!
12. Related patterns
This hones the crucial skill of Question Asking°, and would be a great way to practice different Problem-Solving Methods°.
This would be a great source of problems for a student’s Deep Practice Book°.
If everyone understands how to do a Boss Problem, we might want to celebrate that with a Genius Rock°.
Afterword: Going full-meta, here
I don’t know where to put this story, but Boss Questions is one of the innovations Kristin and I made when we co-taught the upper elementary classroom of a private startup school outside Seattle, and dang did it make math more of a fun challenge for the kids! So much bang for so little buck.
One young woman in particular started working with us in fourth grade with a strong mathphobia. She was bright, she was hard-working, and she was accustomed to being able to get things. When she hit a wall, she’d emotionally shut down.
The Boss Questions freed her, when she was having a hard time, to focus her prodigious powers on something that was still math, but wasn’t the math that was tormenting her. When she left us after fifth grade, she didn’t just excel at math, she actually enjoyed it. Better: a few years later her mother wrote us to tell us this had stuck.
If you use this, and it succeeds or fails, please let me know!
Rovelli’s book is somewhere between “amazing” and “so amazing it hurts”; it tells the story of where Philosophic Understanding comes from (hint: Romantic Understanding). It’ll be coming up more in the future; feel free to read it now.
Provided it’s not a centipede.
I know what you’re thinking, but no, this isn’t Peter Liljedahl the famous Swedish canoeist HOLY CRAP THEY’RE THE SAME GUY! He’s on the Faculty of Education at Simon Fraser University… which was, coincidentally, where Egan taught at. Hmm.
I’m frankly skeptical about this, but one AI product seems potentially amazing — and is intriguingly Egan-ized without knowing the name “Egan”. I’ll be writing more about this soon.
Damned details.






Back in community college I tutored calculus. I usually included one challenge question on each worksheet for my students. But most of the time they ignored them.
They were there to get extra practice to pass their classes, and they knew the challenge problems were harder than anything that would show up on their exams. So they would rather focus their effort on what they knew they needed.
I kept including challenge problems mostly because I enjoyed coming up with them, but it never worked out like I hoped.
Personally, I love the idea of Boss Questions. But it seems like it doesn't mesh very well with the typical class incentive structure.
One more thought - what makes this pattern work for math and not for other subjects?
Is it that math is primarily about solving problems? Is it just that math has right answers? Or is it perhaps that math builds on itself, so solving a single hard question proves that you have a multitude of prerequisite skills?
I can imagine the same strategy working for other subjects like physics that mostly involve math. I don't see how it would work for an English class, but maybe that's just my own lack of imagination. What do you think?