Too often, learning math can feel like working on an assembly line.
A new concept slides in on a conveyor belt; it’s your job to learn it. You acquiesce. After that comes another concept, and you learn that. And then more and more, one after the other. You’re nervous that if you fail at any one of them, you’ll fall behind.
But what if learning math could be like working in an artist’s studio?
What if could choose hard math problems yourself, and learn the concepts as useful tools that help you solve them? What if you could experience the thrill of winning and the ecstasy of making a breakthrough? What if you could labor in the calm satisfaction that the understanding that you’re building will be yours forever?
What if this could — as they say — Completely Transform Education™?
Imaginary Interlocutor: Isn’t this yet another overblown promise from an industry addicted to shilling vacuous hype?
Kinda! But also, kind of not.
Below, I’ll unpack a method I’ve created to help kids (and adults) master math — a tool I call a “Deep Practice Book”. It’s something that I’ve hyped before in the past.
I’m sharing this for two reasons.
First, this tool really is powerful. It’s helped a lot of people, and it can help many more. (You, or someone you know, might be among them.) It’s a great example of how cognitive science can be applied to learning.
But second, it really can’t Completely Transform Education. It’s a great example of the limits of what cognitive science (as it’s usually understood) can tell us about learning — which is something that everyone who thinks about how to make schooling better needs to understand.
And that lesson is bound up in Kieran Egan’s insight into the fundamental problem of education.
The backstory
Nowadays, I’m laboring to create an ambitious science curriculum. But before I got into science, I did something quite different — high-end, high-stakes test-prep coaching.1
A lot of us thrive on extremes: some people get into mixed martial arts; I got into SAT prep. There was no need to fret about classroom management: it was one-on-one, and the students wanted to be there. “How much can I improve my score?” was all that mattered. How clearly could I help a student understand semicolons? How quickly could I help her master percent change? How long could I help her keep all these things in her head?
To achieve all that, I invented a tool. It combined everything I had learned about expertise, memory, creativity, and cognitive science more generally.
I called it a “Deep Practice Book”.
Eventually I presented it in a TEDx talk and a few webinars. Doing this, I discovered that I wasn’t the first person to create such a thing. The redoubtable Michelle Scharfe (if you homeschool, you probably know her site ResearchParent.com) has built her Minimalist Math curriculum on many of the same principles.
The section below is adapted from an essay I wrote a few years ago, to pair with some of those presentations.
If, in the future, you need to study for any math exam, I think you’ll find this useful. (Science and engineering, too — anything analytical, and where the problems require multiple steps.) If you help anyone learn math — as a teacher, a tutor, or a parent — I think you’ll find it useful, too.
And yet, there’s also a strain of “overblown talk” in it that I now find embarrassing: an implication (if not an actual claim) that this could upend math education in classrooms.
Forgive me for it — after the essay, I’ll do my penance and uncover the pit that a tool like this falls into when taken into classrooms by hopeful teachers.
And at the very end, I’ll state frankly how I think Egan schools (and Egan homeschooling) might fill in that hole, and use a tool like this.
The Deep Practice Book:
A simple method that anyone can follow to impressively raise math test scores and cultivate mathematical genius
Part 1: The Proper Care and Feeding of a Deep Practice Book
Collect hard math problems.
Collect the problems that bamboozle you, that frustrate you, that strike you as borderline impossible. Focus on them. Poke and prod them with questions. Stick with these problems over minutes, days, and weeks. Share your questions with others, and see if their answers make any sense to you.
Collect these problems and questions in a single location — a dedicated notebook or binder.
And, above all, habitually re-solve each of the problems once or twice a week — even when you feel like you don’t need to.
As you do this over the next few weeks and months, you’ll come understand each problem more completely than you could have imagined at the outset.
Better still, you may begin to enjoy the very math that used to make you despair. You’ll taste the thrill of really getting something — backwards and forwards, inside and out — and of making it part of you.
Best of all, you’ll discover something important about your human brain: it has very few limits. Mathematical problems that you used to think were impossible for you to understand will become child’s play and intuitive.
Nothing in class will seem beyond you — because none of it is.
At least, this is what I’ve experienced using a Deep Practice Book. If you’re interested in trying one out yourself, read on...
Part 2: The Secret Origin Story of the Deep Practice Book
Mostly, I avoided math in school.
I was always all right at math — good enough to put me a year ahead in my math classes, and good enough that I never had to particularly worry about math. But I never developed a knack for it — and never really enjoyed it.
In fact, when I found myself bored in high school, and decided to spend a year homeschooling myself, I mysteriously lost my one-year-ahead advantage. And in college, I got my one required math class out of the way as quickly as possible. I didn’t even do that well in it, earning a C+, which the instructor was merciful enough to raise to a B–.
I even avoided classes that smelled like math: physics, chemistry, and economics.2
So when I decided to apply to graduate schools, and needed to tackle the GRE, I knew had a challenge in store.
The GRE is the gateway to graduate school. It’s made by the same people who make the SAT: but they make the GRE on the days when they’re feeling mad. Its math problems deal with simple math — there’s almost nothing on it beyond basic geometry — but the questions can be devilishly complex:
(Go ahead — try it! It’s a hoot.)
And here was me, who had been running away from mathematical thinking for a half decade!
I had one advantage: I was already a test-prep coach for the SAT and ACT. I loved helping other people through their math pains — so maybe I could find some fun in working through my own.
I had started off teaching at a tutoring center, and had gotten good enough to strike out on my own. I had seen some initial success — my first student had gotten into Harvard after improving his SAT score 290 points. But recently, something quite troubling had happened when working with two young women for more than a year.
We slogged our way through the entire SAT book, doing more than 400 math questions.
They studied diligently! I tutored competently!
And then, with the real test less than two months away, I bought them each a new copy of the same book. They re-took the first test...
...and got nearly all the same questions wrong.
We were aghast. We were forlorn.
I want to call attention, at this point in the story, to how weird this is. We seemed to be doing everything right — they were studying hard enough, and I was teaching clearly enough. And yet there was almost no change, even on precisely the same problems.
It was right around then that I decided to study for my GRE.
I took my first test, and got a 670 out of 800 in the math. Now, for the SAT, that’d be a fantastic score — somewhere around the 87th percentile. But on the GRE, it was the 48th percentile.
That means, if you randomly grabbed a hundred GRE-takers and put them in a line, with low-scorers on the left and high-scorers on the right, I’d be the 48th guy.
Basically, average.
Ooch.
I was a test-prep coach — my professional image was on the line! I decided to use the blow to my pride as a motivator to study hard. I wrote up a study schedule for myself: I decided to take a half-test every Monday morning for the three months before the real deal.
And I didn’t want to repeat the tragedy that had befallen my two hard-working students.
It was at this point that I did something utterly random, without understanding why I was doing it: I re-copied all the math questions I had gotten wrong from that diagnostic test into a single binder. And on the cover, I wrote (in big, cocky letters) “HOW WE BEAT THE MATH”:
And boy, did I focus on the problems. Because they were in one place, it was natural to.
I didn’t just solve them, I learned to explain them to myself. I made sure I didn’t write down my work or the answers in the binder (because then I wouldn’t really have been able to re-solve the problems), but I made sure to write down the questions I had:
Wait, how do you add fractions, again?
Why does the area for a trapezoid use the average of the top & bottom?
How the heck does that ugly permutation formula work?
By filling the binder with questions, and by obsessing about the answers, I learned the math so deeply that I could have explained it to a third-grader.
And then, as Monday approached, I prepared to take a new half-test.
Basically, I was studying harder. This, I thought, was the way to understand math: he who studies hardest, understands the most. There’s something importantly true about that — but this story is about something more than studying harder; it’s about studying smarter.
The night before the new test, I did a second oddball, I-had-no-idea-I-was-about-to- change-my-life: I re-solved all the problems in the binder.
And was horrified when I got half of them wrong.
Remember: I had been obsessing over these problems the whole week. I had these problems down: I thought I understood them perfectly clearly.
And here, not even seven days later, I got half of them wrong.
This was my first hint that human brains didn’t evolve to do GRE math. Nor did they evolve to do SAT math, or ACT math — nor middle or high school math!
It’s an interesting rule of psychology: those things that the human mind did evolve to do, it does amazingly, almost without prompting. When you were only three, you could walk, talk, and play better than a hundred-million-dollar robot made by the world’s most brilliant engineers.
But things that humans didn’t evolve to do — algebra, for example — take work.
If I wanted to do really, really well on this test, I realized I needed to study in a fundamentally different way than twelve-plus years of schooling had prepared me for. I needed to identify every mathematical idea I found confusing, and put it into a foolproof system that would allow me to understand it — and engrave it into my long- term memory.
Over the course of the next three months, I added problems to my binder almost as if it were my religion. And I did whatever it took to understand them — read answer explanations, pose questions, ask friends.
Most importantly, I re-solved all of them from scratch at least once each week — each and every problem I had previously entered in.
I re-solved them once. Then twice. Then three, four, and five times.
As I re-solved those problems, something delightful happened: I began to get them right, every time. And quickly, too! Initially I struggled with the problems, weaving back and forth inside my brain to figure out what the next step might be. But now the next steps came easily.
Before, I could only see a single step at a time — now, after re-solving the problem three or four times, I could see the whole thing at once. I could chop the problem up into tiny moves, and deal with each of those moves quickly. Sometimes I wouldn’t even need to use paper.
But that wasn’t the best part! Occasionally, while re-solving a problem for perhaps the fifth or sixth time, I’d realize that I had been an idiot. I had been solving a problem by doing a long series of steps — but if I just re-conceived the problem, looked at it from a different perspective, the entire thing would be easy, could be solved in one or two moves. I’d see straight through the method I had been taught in school to the actual mathematical ideas.
Math, I realized, was beautiful. It was elegant. Math was the art of dealing with the world’s most basic ideas.
These insights were thrilling — when I had them, it felt like the sky was peeling itself open and beams of light were shining down directly on me. And I recognized that this was why mathematicians did it: they were chasing the sublime high of mathematical insight.
How often, I asked myself, did I experience this in all of high school? Maybe once or twice.
But now, while I was studying for a standardized test — engaging in perhaps the least glamorous math learning task Western civilization has invented! — I was experiencing these epiphanies once or twice a week.
I had stumbled upon, I realized, a way of dependably building mathematical understanding. And I was seeing it pay off: almost each week, my GRE practice test scores rose. In fact, they rose quite predictably — going up about as many points as problems I had mastered in the previous week.
When I entered in 10 problems, my score went up 10–20 points. When I entered in 20 problems, my score went up 20–40 points.
By the time I took my real test, I counted, and found I had 104 problems entered into my collection. Most of those I had solved a half-dozen times. I understood them backwards and forwards. Each of them had become a tool I could use to solve new problems. And while each of them had started off as an enemy — something I resented, because I had gotten it wrong — each of them had become something of a friend. And on my practice tests that week (full ones) I scored an 800 and a 790.
When I took the real GRE, I scored an 800 — a perfect score. Not bad for someone who avoided math in school.
But better than the score was my newfound sense of myself as a mathematician. I realized that no mathematical concept was beyond me — I could understand anything, given enough time and effort. And I could enter it into a foolproof system, and, by repeatedly re-solving it, comprehend the ideas even more fully as time went by.
And I even liked it! Because to really understand something — to make sense of it inside and out, forwards and backwards — feels fantastic.
Over the years since then, I’ve helped hundreds of students build their own collections of impossible problems — “magical math binders”, as one of my students has dubbed them, or “Deep Practice Books”, as I now call them. And in what follows, I’d like to help you build and maintain your own.
Part 3: What Does Your Brain Need?
Before we go any further, we need to ask one question directly: what does your brain need to crank out genius?
Oh, yes, that word: "genius". We’re talking learning K–12 math here, not painting the ceiling of the Sistine Chapel. We shouldn’t get too romantic. Why not use a more conventional word, like "skill", "ability", or "expertise"?
Because what the Deep Practice Book allows you to do is go much further than just being good at math. It’s about creating your own understanding — and finding pleasure in it!
Mathematical genius isn’t about being a “math robot”, able only to crank out answers to problems you’ve seen before.
Mathematical genius contains that, but goes far beyond it — it’s about being able to quickly answer familiar questions, and puzzle out answers to wholly new ones. It’s about being able to see differently: to spot patterns most people miss. And it’s about enjoying the struggle.
genius = expertise + creativity + joy
And genius is your birthright.
As three-time New York City Teacher of the Year (and present-day educational radical) John Taylor Gatto has written, "Genius is an exceedingly common human quality, probably natural to most of us."
As the proud owner of a human brain, you are the heir to billions of years of neural evolution. You are the direct descendant of millions upon millions of organisms that used their wits to win the evolutionary game.
On top of your body, encased in bone, sits a slimy 3-pound gelatin that is able to pick out patterns, learn from mistakes, lust after elegance, and spawn new ideas.
But in school math classes, you mostly use it to memorize formulas and regurgitate algorithms.
The way we’ve constructed schooling often sells your natural potential short. Just by dint of having a human brain, you're able to do so danged much. The SAT and ACT are opportunities to test this out, to see how much your brain can do, when you understand how it works.
That’s to say that prepping the test is your chance to create a system for doing great things. And to do this, you need to understand what your brain needs.
So: what does your brain need?
A. Your brain needs real challenges
Don't waste your time with problems that are easy for you. The American way of teaching math gives you the method before it gives you the problems: avoid this! Jump into the deep end of the math pool. Seek challenges.
B. Your brain needs to know what it doesn't know
You want to steer toward confusion and frustration — but you don't want to stay there! Systematically identify what it is, precisely, that you don't know. Do this consciously; in fact, write it down.
Much of the expansion of cognitive psychology in the last three decades has happened when scientists began to acknowledge the power of the unconscious mind in thinking. But your unconscious needs help: when you get specific on what it is that you don't understand, you free up your unconscious mind to focus on it.
C. Your brain needs questions
When you isolate something you don't understand, pose it as a question. Questions are borderline magical: they not only help you focus your mind, they also make it easy for you to tap other people for help.
D. Your brain needs immediate correction
Your mind isn't good at developing skill when you separate the "doing" from the "feedback". Imagine trying to improve your ability to shoot free throws by shooting ten basketballs blindfolded, and then having someone tell you the next day which shots you made.
That's crazy, of course. And yet it’s precisely how many math classes are designed: you do a problem, you hand it in, and then you wait until the next day to find out how you did.
So “cheat”: look at the answer explanations! When you're practicing, get immediate feedback.
Your brain needs to have most of what you learn stored in long-term memory. The amount of information you can attend to simultaneously is incredibly small
— only 3–4 items. But the amount that you can store in your long-term memory is huge — no one has yet filled it!
Ever wonder how some people become really good at math? It's not because they're thinking more. On the contrary: they're thinking less.
People who are good at math have built the discoveries they’ve made before into their long-term memories. While the rest of us are re-constructing concepts each time we solve a problem, they’re casually borrowing from their long-term store of memories.
Storing information in your long-term memory will allow you to think less in the moment. It'll save your brain from needing to re-create everything again and again.
And to store this information, you need a system. It's terrifying, but you forget most of what you learn. In fact, you forget it quickly!
Because of this, most test-prep (and most math study in general) is wasted. It's forgotten. It's like building an igloo out of blocks of dry ice, only to have them evaporate hours later.
You can fix this.
E. Your brain needs the basics to be automated
Your attention can only hold onto a few things at once, and it takes some attention to pull information out of your long-term memory.
Sometimes it takes lots of attention to remember: like when you have to squeeze your eyes shut to recall: what was the name of your kindergarten teacher? Other times, it takes almost no attention to remember: what is your middle name?
The information you recall a lot has been "automated" — made into a reflex. In order to deliver genius, your brain needs to have the basics of test-prep math automated.
F. Your brain needs multiple methods to understand a problem deeply
Genius comes when you understand the deep structure of a math problem — what it looks like on its most fundamental level, beyond its superficial features.
The trouble is, you can't just tell your brain to get that sort of understanding. "Trying harder" won't produce it.
There is a method that helps: find multiple ways to solve a problem.
See if you can solve a problem with algebra. See if you can solve it by plugging in your own numbers. See if you can solve it by drawing pictures. See if a friend has a different way to solve it!
By understanding multiple methods, your brain will be able to see the deep structure of the problem.
Part 4: How to Build a Deep Practice Book: 5 Steps
Over the last decade, I’ve taken my own experience of building a customized binder of math problems and re-created it — always iterating, tinkering — to help my students do what their brains need.
I’ve come to call the results a “Deep Practice Book”.
A Deep Practice Book (or “DPB”) is a personally-chosen collection of math problems that you ask questions about, understand clearly, and regularly re-solve. You can make a DPB out of notebook paper — I used to have students do just that. The very simplest version of a DPB doesn’t require extra paper at all — it’s just a list of problems you don’t understand, pose questions about, and keep re-solving.
Over the last five or so years, however, I’ve found that it helps my students to have a pre-made version of the DPB made for them, so all they need to do is fill in the blanks. This means that they don’t need to perfectly understand all the reasons behind the DPB in order to start using one. But you can make a simple one in a cheap notebook.
But whatever format of the DPB you use, its five basic steps are the same:
Find lots of problems you can’t solve
Fill the DPB pages with ‘em
Learn to teach the problems
Ask for help
Re-solve the problems regularly
Each of those deserves a little explaining.
Step 1: Find lots of math problems you can’t solve
If you’re planning to take the SAT, I recommend getting a copy of The Official SAT Study Guide and working through the math problems in the first third of the book, before the sample tests. They are about a hundred of them, and they’re representative of the sorts of math questions that will be on the actual SAT. (They’re also quite hard, so if you do especially poorly on them, don’t feel forlorn!)
If you’re taking the ACT, I recommend getting a copy of The Official ACT Prep Guide.
If you already have a different source of math problems, by all means, use it — just make sure that it’s geared toward the test you’re going to be taking.
Particularly good additional sources of math problems include:
Virtually any test-prep book for your test, be it by Barron’s, Kaplan, Princeton Review, Ivy Global, or McGraw-Hill. (I’m currently using Dr. Jang’s SAT 800 Math Workbook for the New SAT for my own SAT study.)
Any particularly devilish problems you encounter in your high school math class. (You know those one or two questions at the very end of your test — the ones that the teacher throws in just to make you squirm? Those are perfect.)
A note: since the SAT has been redesigned, both tests are now much more similar than they are different, and nearly all of the mathematical insights you’ll gain working on one test will help you with the other. When you study for true understanding, it helps in all sorts of situations! That said, because there are slight differences, you’ll want to use problems from the test you’re preparing for.
After you find a source of problems, do lots of them — and mark every problem you don’t perfectly understand.
That means draw a star next to every problem you get wrong, every problem you get lucky on, and every problem you skip.
And now’s the time I need to admit something personal.
I get lots of problems wrong. And every time I do, it feels horrible.
It feels like failing.
It feels like the end of the world.
Before I started keeping a DPB, I felt this frequently, and tried to suppress it. Frankly, that never worked.
Now that I keep a DPB, I’ve learned to accept those feelings — even embrace them. I know that, since I’ll be adding the problem to my collection, I’ll be mastering it. I’ll be using it to jujitsu math! No matter how impossible the problem seems now, it’ll become a tool for me to use to get more problems right in the near future.
I’ve learned that — as unlikely as it typically seems in the moment — each of these problems will become something I actually enjoy.
Daniel Coyle cites a German proverb at the beginning of his excellent book, The Talent Code:
You will become clever through your mistakes
It’s really terrible, I remind myself, that in America we’ve defined “a good math student” as someone who doesn’t make mistakes.
Keeping a collection of problems you can’t initially solve is the way to reverse that. Great math learners are people who make tons of mistakes, embrace them, and learn from them.
Step 2: Fill the Deep Practice Book with these problems
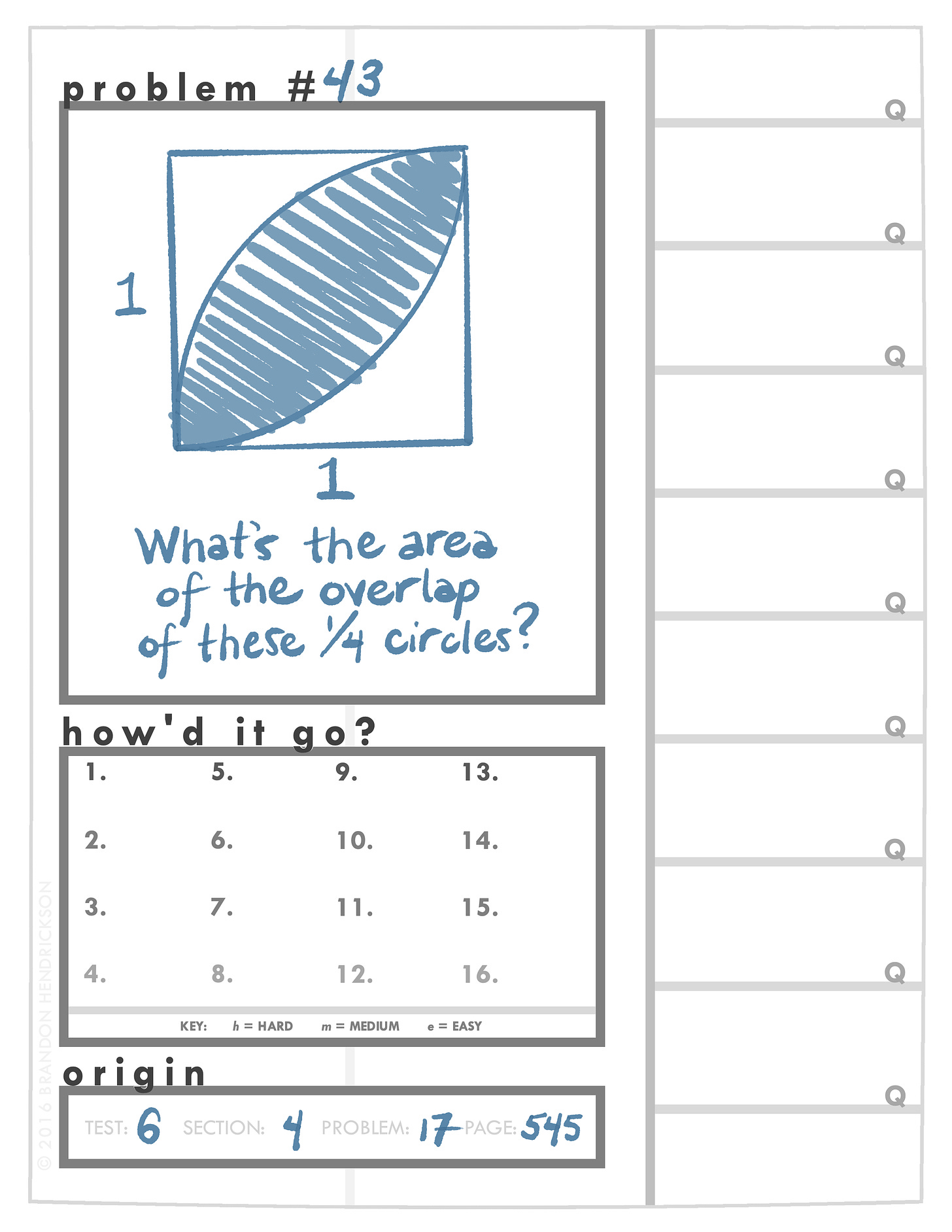
Here is what one version of a DPB page looks like. In this version of the DPB, pages are double-sided. Here’s the front —
And here’s the back —
Before you do anything else, fill in the origin of the problem — where you’re getting it from. Depending on where you found it, that might mean:
the test number
the section number
the problem number
the page number
the title of the book / the URL of the website
Then write in the problem itself. This typically takes a while, but it’s worth it: recopying the problem leads you to pay attention to all the details. (Oftentimes, you’ll get a problem wrong because you didn’t see a word like “NOT” or because you misread the labels on a geometric figure.)
Spending a minute or two just writing the problem down (or three, or four!) also gives your mind a chance to half-relax, which can be a great state for creative thinking. (Often it’s only when you stop trying to force a solution that the solution appears.)
Because I’m particularly sensitive to beauty and ugliness, I make it a point to copy in problems as neatly and elegantly as I can. But if this doesn’t matter to you, write it however you’d like — just make sure it’s clearly legible!
Anyhoo, it could look like this —
Q: Should I write the problem in word-for-word, or can I paraphrase to make it shorter?
A: That depends!
Did you get the problem wrong because you didn’t understand what it said? In that case, you’ll definitely want to enter it in word-for-word. (Otherwise, you’d be making the problem easier, which would render it less useful to put in your DPB!)
But did you get the problem wrong for some other reason? In that case, yes, by all means paraphrase!
Whatever the reason was that you got it wrong, personalize the problem whenever you can. If the problem uses names like “Carlos” and “Alice”, I might replace those with “Eric” and “Kirsten” — names of my high school friends. If it talks about serving orders of “hamburgers” and “French fries”, I might replace them with orders of “crickets” and “giant centipedes”. I’ve had students replace some pretty boring details in word problems with risqué stuff... the details of which [shifts awkwardly in chair] I won’t repeat here!
But you’re going to be spending a lot of time with these problems. Go ahead and make ‘em easier to love.
And be sure to fill in the correct answer — on the back of the page. When I created my initial version of the Deep Practice Book, I didn’t actually write in the correct answers, or the origins. I got lucky, and this didn’t spell doom for me. I was able to recall where each problem was located — so I just looked up the correct answers again and again.
But what a waste of time! And a dangerous practice, it turned out. When I had one of my students make his DPB, he neglected to consistently look up the book’s answers. When he re-solved the problems in the future, and got them wrong, he just assumed he’d gotten them right — which meant that he was training himself to get problems wrong.
Ack. It would have been better for his mathematical understanding if he had just spent the time watching TV.
So: make sure you write the correct answer on the back of the page. And, of course, don’t write the correct answer on the front of the page. If you did that, you’d see the correct answer while you were re-solving the problem — and you’d be perpetually tempted to say, “oh yes, this is the correct answer; of course I understand this...”
Step 3: Teach the problem to someone else
Now that you’ve entered the problem’s basic information into the Deep Practice Book, your real task begins: understanding the problem well enough that you can teach it.
Right now, of course, you probably have no idea how to do this! (If you understood the problem to begin with, why did you put it into your DPB?)
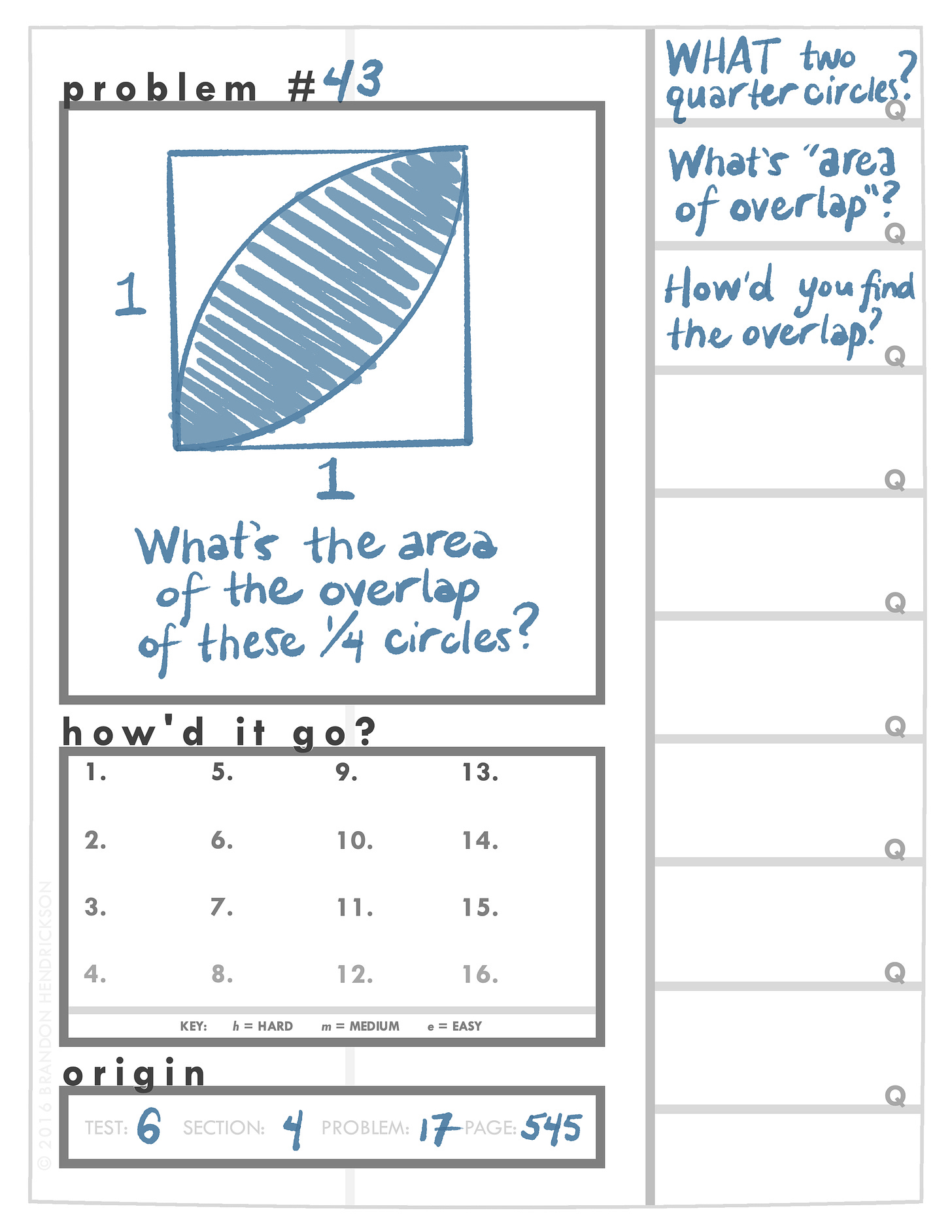
The first step is to ask as many questions about the problem as you can think of. The questions can be of any sort:
You can ask about the meaning of a word: “What does ‘prime’ mean?”
You can ask about a problem-solving strategy: “How can I quickly figure out if
1,002 is prime?”
You can ask about a specific math concept: “Is 1 prime?”
You can ask about a larger math idea: “How many primes are there?”
The only qualification is that your questions have to be questions you actually want to know the answer to. This isn’t the time for you to show off with how brilliant you can sound — typically, the dumber the question, the more helpful it is! (My own most common question is some version of WHERE WOULD I EVEN START WITH THIS?!)
Q: Question-asking! Is that stuff actually important?
A: It’s tremendously important (and nice question)! Mathematics, at its core, is the art of question-asking. American schooling, however, has twisted it into instruction-following. To honestly ask questions is to engage in a little bit of real mathematical thinking.
Don’t try to hold the questions up in your head — write them down onto the front of the page, on the right-hand flap —
As you discover the answers to the question, write them on the back of the flap. (Note that the flap is, ah, a “flap” — it’s designed to be folded. That way you can quiz yourself on your questions, without spoiling the problem by seeing the correct answer.)
Maybe just asking and answering the questions triggered you to understand the problem clearly. If so, huzzah! If not, don’t fret — move onto the next step.
Read the book’s answer explanation. If today’s your lucky day, you’ll understand it immediately. Much more likely, however, you’ll hardly understand a word of it. (It’s incredibly difficult to write an explanation that makes sense to students of different levels.)
Again, don’t fret — start writing down more questions on the flap about the answer explanation. For example:
“When the explanation says ‘complete the squares’, what does that mean?”
“Why does the book say to add 16 to both sides of the equation?”
Attempt to teach the problem step-by-step by writing it down. Use the “Teach It” section on the back of the DPB sheet. Try to do this even if you don’t entirely understand the problem yet — see if you can walk someone through the steps you’re reading in the answer explanation.
Q: Should I imagine teaching this to... myself? To another person?
A: Explain it to yourself! To a friend! To a giant duck!
Once upon a time, I actually included a picture of a giant, inflatable duck in each page of the DPB, and instructed students: TEACH IT TO THE DUCK!
This, frankly, seems crazy now. I wonder why I ever thought it was a good idea.3
If it helps you imagine teaching this to another person, do it! If it helps you to imagine teaching this to yourself in 4th grade (because: time machines), do it! And if it helps you to imagine teaching this to a terrifyingly large imitation waterfowl, go ahead and do that.
But don’t just write down the mathematical steps — write down the reasons you’re taking those steps in words.
Write the math in the left column, and the reasons in the right. You don’t want to just memorize steps — you want to understand why you’re taking them.
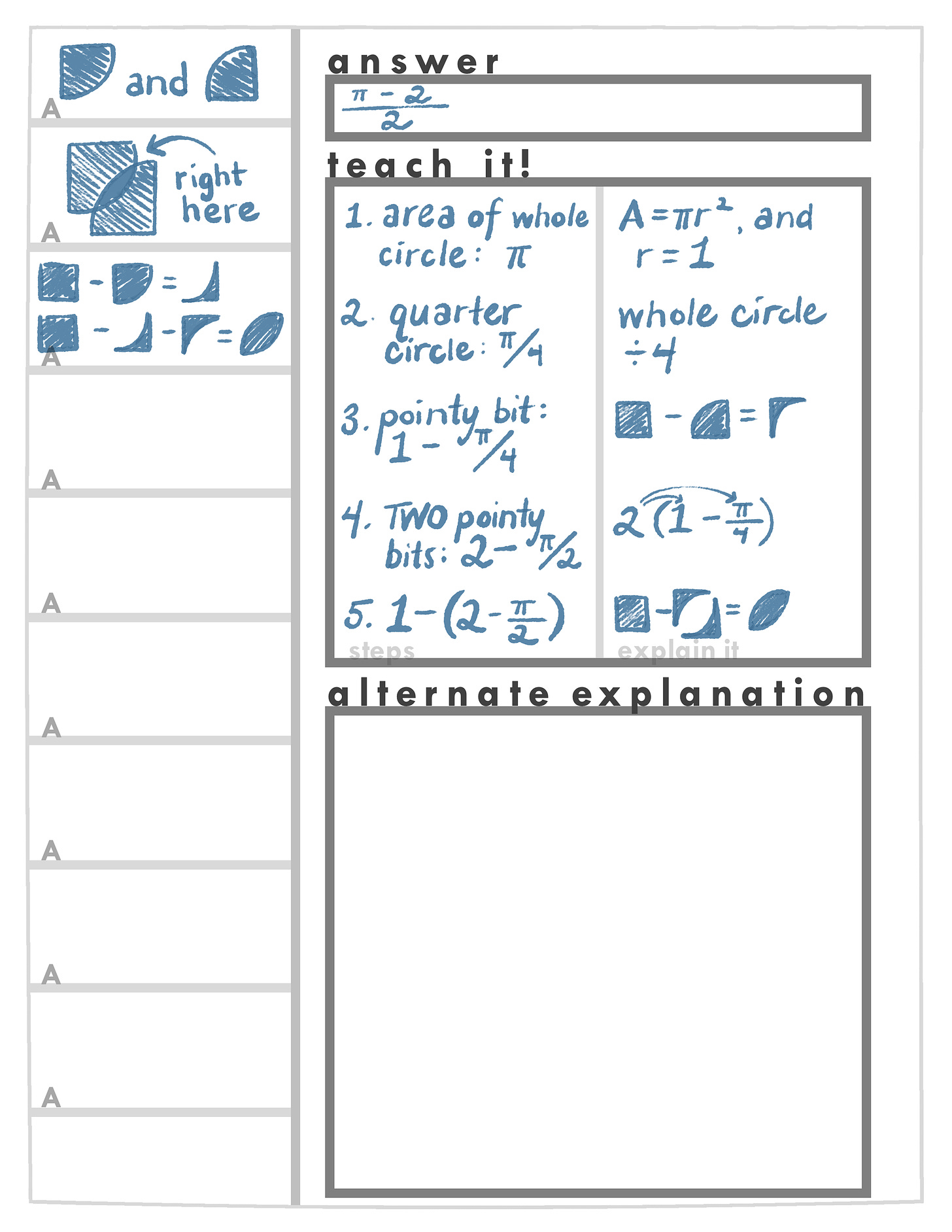
What if you don’t understand why your book says to take a certain step? Write the math into the left column, and just leave the right column blank for the moment. Again, turn your confusion into a question, and write it down on the question flap (“What do they mean when they say...?”). Every question you ask, you can find an answer to! You’ve got a human brain: you can understand everything.
Q: So is this like writing a two-column geometry proof, when we give the statement and the reason?
A: Oh heavens no.
Now, yes, there is something superficially similar about the format of the Deep Practice Book’s “Teach It” and that of the two-column proofs you did in geometry class: if you squint hard, they look the same!
But the purpose of the DPB’s “explain it” column is to help a real human being (or, ah, an inflatable duck) understand it. The same can’t be said of a math class proof.
In the DPB’s “explain it” column, you can use casual language. You can use pictures. You can even use obscenities — do whatever you need to help another person solve the problem!
What are you allowed to use in a geometry class’s two-column proof? Oh goodness.
Let’s be perfectly clear about this: the format of the two-column geometry proof is soulless and bureaucratic and horrible and terrible and really not very good. It pretends to be an education in real mathematical thinking, when (as mathematician Paul Lockhart famously complained about in his hilarious, piercing 2003 essay, “A Mathematician’s Lament”) it’s really just training about how to obsess over piddling details. What’s lost is any sense of the elegance of real mathematical ideas.4
So, yeah: both of them have two columns! Otherwise they’re totally different.
Step 4: Ask for help
You don’t need to go this alone: now that you have specific questions about these problems, you’re ready to ask other people for help.
What kind of people? Math teachers, for one. (We’re not as scary as we seem. And most of us got into this job because we really, really love helping motivated students understand math!) Math-y relatives, for another. Tutors, if you have access to any. Friends are always a good resource. Even acquaintances — say, that kindhearted person sitting to your left in class — can be helpful.
People love to help. And asking others for help, amazingly, makes people like you, even if they hated you before.5
When you find an answer, write it down on the back flap!
Step 5: Re-solve the problems regularly
Finally, for what might be both the most important and most counter-intuitive aspect of keeping a DPB: regular re-solving. Why?
You might assume that once you break a problem apart, understand each of its parts, and put it back together, you’d remember it.
You might also assume that, once you obsess about a problem, and teach it yourself, you’d remember it.
I, too, once assumed as you do! Oh my goodness was I wrong.
Recall my experience entering in GRE math problems into my first DPB: even though I understood them perfectly, after just one week I had forgotten half of them. Knowing what I do now about human psychology, this makes perfect sense: we’re built to forget. The half-life of most memories is quite short.
But if you want to secure something in your mind, there is a solution: repetition. Repetition, that is, of a certain kind.
First, the repetition must be active. Re-reading something (a textbook, a math question, a correct answer) isn’t very useful in securing it in your memory. If you want to remember how to do a math problem, you actually need to re-solve it, on scratch paper.
Second, the repetition must be spaced. (Wikipedia’s article on “the spacing effect” is a good introduction to this.) Lots of repetition over a short time fails to fasten knowledge into your memory — lots of repetition spread out over a long time succeeds.
I set aside one day each week to re-solve all the problems I’ve copied into my DPB. You may find that, at first, you want to re-solve each of the problems twice a week.
Each time you re-solve the problem, record how well you understand it in the “how’d it go?” section, with a letter —
write “I” for “impossible” (if you’re still trying to understand the problem)
write “H” for “hard” (if you can get the answer, but are trying to understand all the steps)
write “M” for “medium” (if you understand the steps, but they come only when you put some effort in)
write “E” for “easy” (if your understanding of the steps comes fluently, but you don’t understand the problem as a single whole)
write “A” for “automatic” if you can see the entire problem in your head
“Fluent”, here, means “I don’t need to bang my head against a table to figure out how to solve it.” And “automatic” means “I can see all the parts of the problem in my head at once — I barely even need a pencil and paper to solve this!”
Q: Won’t this “regular re-solving” take a really long time once I have, say, 50 or more problems in my DPB?
A: It will not! And that’s the beauty of the thing.
When you first attempted one of these problems, of course, you simply couldn’t understand it. (That’s why it’s in your DPB.) As you began to understand it, you could do it more and more quickly.
After you successfully solve a problem a handful of times, however, you become amazing at it, and you can do it almost instantaneously. It’s automatic.
It’s at this stage that you really understand a problem. And because our society has done a terrible job designing K–12 math instruction, most students rarely get to this level. Instead, math class feels like a conveyor belt: the problems you don’t understand drop off the end, never to be attempted again.
Which is such a shame, because you can understand them perfectly. All you need is a little more time.
When you blow through twenty previously-impossible problems in five minutes, then you’ll experience the power of the DPB — which is to say, the power of your own brain, when you give it what it needs.
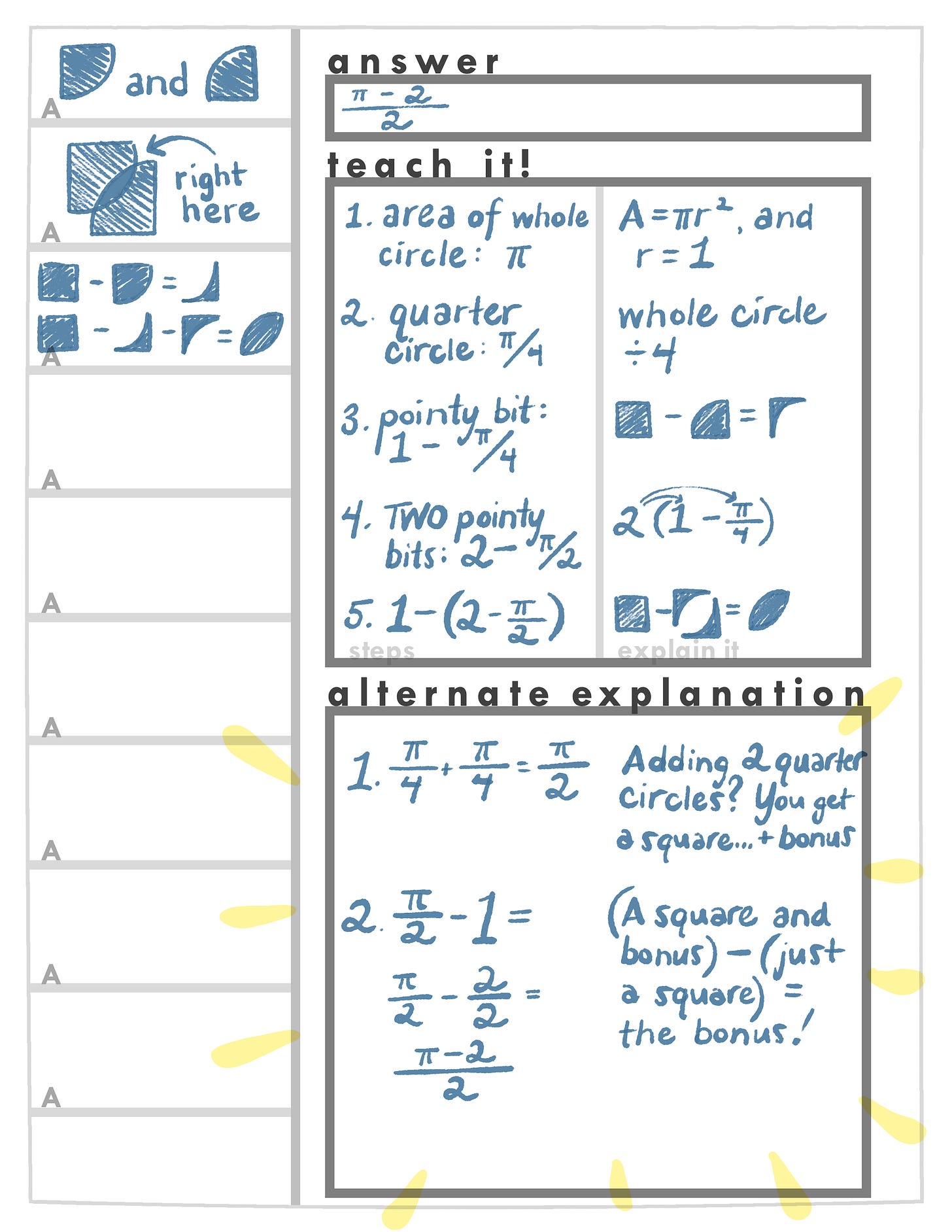
Q: What’s with the final rectangle — the “alternate explanation” part on the bottom of the back page?
A: Save these for your moments of brilliant insight, when you realize there’s a much more elegant way to solve the problem.
Not all problems will get a second explanation method. Sometimes, you’ll just get really good at solving a problem one way. And this is enough — this is great!
But every once in a while — for me, it happens once or twice a week — a new way of solving a problem will suddenly come to you. And when that happens, math is glorious. You’ll realize that your previous way of thinking was superficial, that what’s really going on in the math problem is more simple (and beautiful) than you could have seen before.
And there is, perhaps, no other way to reach this level of understanding than to approach a problem again and again, picking at it with questions.
This is so different than the way schools have been set up since the late 1800s. They’ve been designed around deliberate thinking, as if that’s the only trick brains can do. In his book Hare Brain, Tortoise Mind: How Intelligence Increases When You Think Less, Guy Claxton suggests that this leads us to miss our true potential:
“If we see d-mode as the only form of intelligence, we must suppose, when it fails, that we are not ‘bright’ enough, or did not think ‘hard’ enough, or have not got enough ‘data’.... What we do not learn is that we may have been thinking in the wrong way.”
Part 6: What to Do Next
Now that you know how to build a Deep Practice Book, go ahead and start!
You can simply buy a notebook, and draw in the elements yourself. Or you could print out these empty pages, and pop ‘em into a three-ring binder. Or you can make a copy of this Google Doc, and try entering ‘em into it.
Or, heck, you can just start by looking at the last test you took, and drawing stars next to the problems you’d like to master — whether you got them wrong, or just found them more difficult than you think.
Because here’s the thing: human minds weren’t built for math, but we do have the ability to master this stuff. And when we do, it feels amazing. This is your birthright as a human being — all you need is the right structure to do it.
Okay: we now return to our regularly-scheduled substack post.
Where’s the Egan?
None of the above Deep Practice stuff is based on Egan; it’s based on mainstream brain science. (If you’d like a more rigorous explanation of the idea, with fancy citations and terminology that leans more towards phrases like “cognitive psychology” than “brain science”, you can read another essay I wrote here.)
That’s not to say that it’s all cold, calculating, and Vulcan-y: cultivating a Deep Practice Book is an emotional roller coaster. After a lifetime of being pretty good at math but never seeing what all the fuss was about, building a Deep Practice Book for my GRE prep was what made me actually fall in love with math.
But it’s still not Egan-y: where (for example) are the stories? Where are the metaphors? Where is the wonder and awe?6
This isn’t built on Egan’s paradigm, and this substack is all about how Egan’s paradigm can open doors toward new kinds of education. So why am I sharing it here?
Where’s the pit?
Remember before when I said that a tool like the Deep Practice Book couldn’t transform the classroom math experience — that it (and tools like it) is doomed to fall into a pit and crash and burn when it enters the classroom?
Well: what’s the problem?
Pretend, for a moment, that the Deep Practice Book really is the One True Way to learn math.7 Imagine that it works even better than I’ve suggested. Picture a world in which all the students who make Deep Practice Books get a rich understanding of math, get straight A’s in chemistry and physics and engineering, and grow up to become scientists who cure obesity and acne and male-pattern balding.
What’s missing from this picture?
Very few students will ever make a Deep Practice Book.
It’s hard. It focuses you on your failures. It takes time. You can only do it if you really want to improve your mathematical abilities. That means it’s absolutely not the sort of thing that students can be forced into. If you try, you’ll find students going through the motions, and getting none of the benefit.
(In this, it’s much like Anki, the spaced-repetition flashcard program that I use as an add-on for my classes, love desperately, and once totally failed to get Kieran Egan excited about. And, just because we’re on the topic, if you’re a fan of spaced repetition and you haven’t read tanagrabeast’s essay “Seven Years of Spaced Repetition Software in the Classroom”, you owe it to yourself to: it’s one of the wisest pieces of educational writing that I’ve ever read.8)
Because of all this, a Deep Practice Book isn’t the answer to any of schooling’s challenges. While parents and tutors (and perhaps especially homeschoolers) can help kids create their own DPB’s, when it comes to classroom teaching, a DPB can at best spotlight some principles of learning that can improve math education at the margins.
So many educational innovations are in this same bucket: built on good ideas, but useless at bringing about the fundamental changes we want… because they’re missing the most important piece of learning.
The missing piece
What’s missing, for most students, is desire.
If a student wants to build mathematical understanding, something like a DPB can help them step off the assembly line, stop forgetting what they work hard to learn, and start asking questions. It can help them become agents in their own education.
But, for math, most students lack the desire to do this. And that’s due, in part, to how we understand what “teaching math” means.
In the first content-heavy post of this substack (“The Hole in the Heart of Education”), I wrote that
the matter with schooling is that schooling doesn’t matter.
Especially in the early grades, “teaching math” means to mastering skills and learning knowledge. But for mathematics to matter for most kids, “teaching math” needs to be something quite different.
What would Egan have us do? Help kids enter the story of math.
The story of math
We should think of math as an adventure to join. Part of that requires that we start to tell kids the millennia-long epic of how humans created math, and the powers it unlocked — for good and ill. (I wrote about this a bit in my ACX book review of Egan’s Educated Mind; search for “elementary math” and “middle school math”.)
We can start, in kindergarten and early elementary school, with Stone Age humans struggling to exist in the world, mathematically armed only with (perhaps) a mammal’s sense of “one”, “two”, and “many”.9 We can show them baboon bones that suggest humans invented new words to focus their minds on larger numbers, and the Sumerian tablets showing wedge marks capturing those ideas in clay. And we do more than tell these stories — we can help them do the activities that laid the foundation for later mathematics.
We can help them feel the awe that ancient astronomers might have felt when they discovered the power of math to predict the events of the heavens. We can spark in them the dread of the tyrannical rulers of early states who discovered that the mathematics of land surveyors and censuses could help them better control their populations.
In middle school we can tell them of the birth of Greek mathematics when the out-of-work Babylonian magi trekked west to teach their math (and astrology!) to the Greeks. We can lavish praise on the genius of Archimedes, whose clear-headed insights into the mathematical predictability of mechanics gave birth to a worldview that would be brought back to life, millennia later, by Galileo, to help make the world modern.
And even (in high school) postmodern — we can help them explore questions like “what’s bigger — infinity, or infinity times two?” and see how Canton’s discoveries caused other mathematicians to shake their heads. We can help walk them through the Barber Paradox, and see how Gödel’s incompleteness theorem caused his fellow logicians to despair of whether it’s possible to know anything at all.
Imaginary Interlocutor: Oh my gosh, are you saying that…
Let me be clear about some things I’m not saying. I’m not saying we should only tell kids stories for math. (That would be idiotic. They need problem sets, too.) I’m not saying learning math should be only pleasant. (They need struggle, too.) I’m not saying we should jettison the ladder of math progression — counting in kindergarten, long division in fourth grade, hyperbolas in tenth grade — and make content an anarchy. (A legible ladder of progression seems incredibly useful.)
What I’m saying is that to turn classrooms into cultures that value mathematics, we need to approach the curriculum as an opportunity to join one of the big adventures of humankind. Egan’s approach makes this possible, because his tools (e.g. stories, metaphors, wonder and awe) are the things that cultures are built out of in the first place.
And when math matters to students — when they desire to understand it better, and are willing to work hard to do that — then tools like a Deep Practice Book become things that more kids will be happy to start using, because it makes that easier.
Egan’s method, in other words, isn’t enough. But it’s something better: the door that opens into all sorts of new educational possibilities.
I used to keep mum about this when around educators. In some teacher circles, “test-prep coaching” has the same moral resonance that “narcotics-officer-turned-meth-entrepreneur” has in policing circles.
Such regrets! Since graduating college, I’ve fallen deeply, desperately in love with the sciences. And coming to them late in life does have its advantages…
Note from Brandon in 2023: it’s amazing that I had forgotten the origin of this: every coder everywhere.
Wait — you mean you haven’t read this essay yet? You’ll love it! If we ever do a substack reading group, this will be one of the first things we discuss. For Lockhart’s fair and balanced critique of proofs, skip to the section near the end titled “High School Geometry: Instrument of the Devil”.
This is called “the Benjamin Franklin Effect”… and it might be more useful than everything I taught my SAT students.
Typing this now, I wonder if the reason that when a Deep Practice Book works, it works because it generates some of these things. I still remember some of the stories of how I mastered some of those 100 problems. When I really grokked a problem, I’d sometimes see it as a metaphor for solving another. And I was repeatedly led to experience awe over the simplicity behind the formulas I had memorized in school. Still, if we call this “Egan”, then I fear that we could call almost anything that worked “Egan”, and that seems unhelpful.
It’s not.
If we ever do a substack reading group, this will be one of the second things we discuss.
Is this true? I’ve seen it attacked: xkcd.com/764/







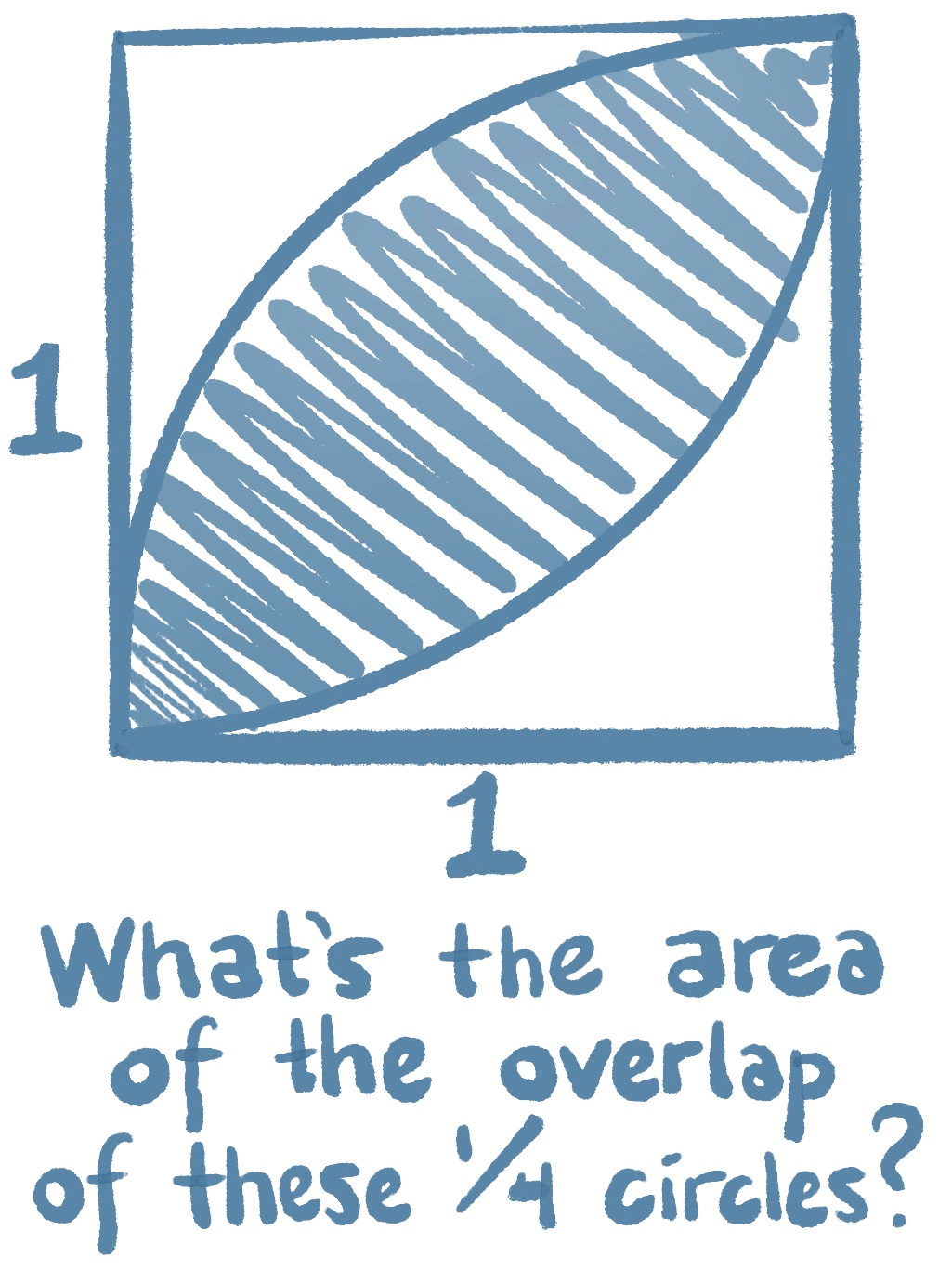








I realize the SAT wasn't really your main focus here, but there's an argument I've heard occasionally within the rationalist community that goes something like this:
1. IQ is virtually impossible to train.
2. The SAT is basically an IQ test.
3. Ergo, we should expect SAT prep courses to be mostly ineffective. Very few people will be able to raise their score dramatically.
It sounds like you would disagree, right? Do you think most people are capable of getting a perfect score if they use your Deep Practice Book method?
Math aesthetics are so funny. I made sure to tackle the problem before reading on, and was so surprised you'd written it as (pi - 2)/2 when it seemed obviously pi/2-1 to me!
One possible extra step for solving is thinking about how to "sanity check" your result. Once I did my geometric thinking, I wanted to make sure that pi/2-1 was in fact going to be between zero and 1!