
1. A problem
“7” doesn’t look like the number seven. “+” doesn’t look like adding. “×” doesn’t look anything like the multi-step function that it symbolizes.
One of the reasons kids struggle with math is because it’s so abstract — finicky rules about arbitrary squiggles. And this is especially bad at the very foundations of mathematics.
2. Basic plan
Introduce kids to the Western abacus when they’re young. Use it to help them see that arithmetic means “doing stuff with things”.
Start by helping them use it to represent numbers. Then help them use it to add and subtract. Then help them use it to multiply and divide.
3. What you might see
A first grader squinting at a set of rods & beads, raising her hand, and saying: “one billion, seven hundred eighty-two million, sixty-nine thousand, forty… two?”
A second grader moving beads around to figure out 7,359 minus 5,891.
Third graders exposing patterns in our base-ten system: how do you divide a number by 100? How do you multiply by 11?
Alongside all of this, kids learning to do pencil-and-paper math, and seeing through the symbols to understand what’s actually going on.
4. Why?
If you only know one way to do something, you don’t really know what you’re doing! Learning to use an abacus offers an easy way to see arithmetic in a radically different way.
5. Egan’s insight
Where do we see this in the human experience?
Abacuses1 have been used since ancient Sumer; just on the basis of Chesterton’s Fence, we should be wary to diminish their place in the curriculum.
How might this build different kinds of understanding?
We might imagine that arithmetic can be done anywhere on a spectrum:
I’m thinking that this seems to mirror SOMATIC (🤸♀️) to PHILOSOPHIC (👩🔬)… though Egan didn’t originally create his paradigm for math, so maybe something cooler is going on.2 (What do these weird emoji mean?)
If this is the case, then an abacus might lie in the happy “Goldilocks zone” between the two extremes: it makes abstractions into wooden balls, but makes it easy to do real base-ten arithmetic easily. And it does it through 🧙♂️METAPHORS: each bead is an integer, each rod is a place value.
6. This might be especially useful for…
Kids who have a hard time holding new concepts in their heads, but whose fingers can fly.
7. Critical questions
Q: This isn’t new. EVERYONE knows about abacuses.
But do they use them? Typically, they’re sold as “educational toys”. Everyone slides the beads around on them, but literally no one uses them for math.
Q: “Literally” no one uses them? How could you even know that?
Because they all have the wrong number of beads.
Q: …what?
Each bead is a positive numeral. Our number system has only has nine positive numerals. Seriously, count them: 1, 2, 3, 4, 5, 6, 7, 8, 9.
Q: What about zero?
Zero isn’t a positive numeral. It’s a placeholder; it’s supposed to mean “there are no rocks/puffins/beads here”.
Q: Okay, what about ten?
Ten isn’t a positive numeral. It’s two of them smacked together: “1” and “0”. The whole point of our base-ten system is that you start over after “9”.
Any abacus that has ten beads on a rod was made by someone who wasn’t even trying to create a mathematical tool.
Q: What were they trying to create?
Fidget toys. Sometimes, avant-garde home décor:

Q: How many beads should an abacus have, then?
Nine.
Do you spy a deeper logic in these pretend-abacuses? Would you like to defend their honor? Frankly, WE WOULD LIKE TO KNOW ABOUT IT. Become a subscriber and join in the comments conversation.
8. Physical space
At home
Wanna help kids around the world see math clearly? Help us find a basic abacus that only has nine beads per rod. Or help us find one that we can disassemble, and take a bead off.
If you can find either of these things, please tell us in the comments! (I might make a separate post calling attention to this. It might also make it into the book.)
In a classroom
Ideally, every student would have an abacus — that it would be theirs might emphasize the emotional connection.
It’d also be nice, though, to make a giant abacus that everyone could use together:
9. Who else is doing this?
Someone else has noticed that all the abacuses are fake, right? I can’t be the first person to notice this, right? (Or: what am I missing?)
How might we start small, now?
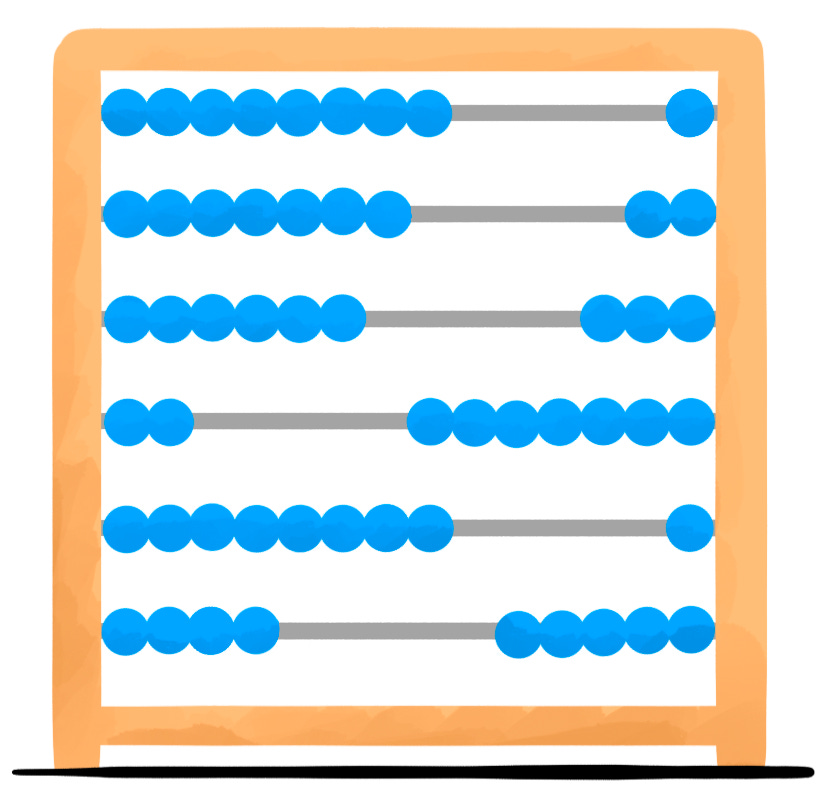
What number is this?
Once you figure it out, see if a nearby kid can. Then, buy a cheap ten-bead abacus, Sharpie-marker the leftmost one black (it’s dead to us!), and ask them to stump you.
10. Related patterns
After this pattern comes FINGER MATH°, which is much faster than an abacus (and which you only rarely need to grab off a shelf).
Wondering why we’re focusing on Western abacuses? The answer is: they sort of suck! The modern Japanese sorobans are much better for calculating, which is why the very next pattern in this chain is BEAD COMPUTERS°. All of this will culminate in FREAKY MENTAL MATH°.
In truth, none of these are exactly better than using a pencil and paper — each has its strengths and weaknesses. More importantly, each is a way to represent numbers and operations. The power comes when kids get MULTIPLE REPRESENTATIONS°, and can glimpse the abstract reality that connects them all.
Afterword:
“Egan and ChatGPT Walk into a Bar” went quite well last night — folk liked it (some reported being amazed), I had fun, and I’m thinking this is a good way to help folk understand Egan. I’ll probably be repeating it in the next week, and perhaps beyond.
In Learning in Depth news, we have a bunch of new sign-ups! The $300 off discount will last for the next seven families to join. Oh, we offer an international discount (our “Big Mac discount”), I probably should have said that earlier.
For years, I’ve been kicking around notions of what the world’s first actually good abacus might look like. If anyone can find a Western-style abacus with only nine beads (or one that allows a bead to be removed without hurting oneself), I’d love to make a post with instructions on how you can create this best-of-all abacuses. (Working title: “Your Abacus is Wrong… and how to fix it”.)
Cool people say “abaci”, but I am not cool.
I’d bother Alessandro with this question, but he’s busy with his dissertation. If any other math-loving Eganheads have a sense of whether Somatic and Philosophic maps onto this, tell us in the comments!







For an overabundance of ideas on the concept of zero, Charles Seife wrote a wonderfully engaging book titled "Zero: the biography of a dangerous idea." If you are looking for a book to help translate Math into English, Ben Orlin's newest book, "Math for English Majors," is equally fantastic as all his others. (My favorite of his books is "Change is the Only Constant," as it so clearly illustrated to me the beauty of the philosophy of calculus, tho I don't claim to be able to use calculus for any purpose.)
I could go on about math books and math education (but not actually about math) for a significant time, but what I came here to say is that a numeral is a figure, symbol, or group of figures or symbols denoting a number. No numeral is either positive or negative: they are all symbolic. The base-10 system necessarily uses 10 numerals to denote its numbers. When "0" is used in conjunction with "1" in the proper order, the numerals together denote the number ten.
The 10-bead-per-bar style abacus, popular with young learners in the west, uses beads, not numerals, to represent the way we group our numbers in tens for counting. The beads (or stones or marks in the dust) may also represent anything else you choose: seeing as this style of abacus is most efficiently used for mere tallying, there is no need to use the middleman of "number" when keeping track of how many games of Sorry I've played in a row on the abacus. I can just say, "I'll play one row of Sorry games today and no more." If you know I'm using an abacus with 10 beads per row and you know your numbers, you'll know I mean 10 games. Otherwise, you'll know when we're done because all the beads are moved. (Tho if we're playing Sorry, you know your base-10, so that was a poor example.)
The number of beads on the bars of this poor abacus you seem to find so offensive (your offense is likely the only reason I am defending it, as I agree there are more efficient styles) aligns nicely with the number of fingers on our two hands. You have kindly failed to point out that every child counting on their fingers has, likewise, been born with the wrong number of fingers to count in a base 10 system, and that for this reason we all ought to be counting base 11. Wait, whaaat? Yes, thank you; most people would find that sort of imposed mathematical conversion traumatizing.
And speaking of imposed mathematical conversion, I will conclude with a story of one of my favorite people: my mom. The household abacus with 10 beads per bar was missing, and all my dad could find was the silly little abacus with 5 beads per bar. "I can't count my exercises on this; there's not enough beads," he said. She replied, "Just count in base 5 and you'll be fine."
My 10-fingered children play with many formats of abaci.
So much to love here!
A very deep truth in education is that people don't stumble so much because things are hard, but because things are abstract. The bit that catches people out in math is not logical thinking or manipulating numbers, but the level of abstraction. Many adults struggle on the Wason selection task, until you phrase it in a specific context (see the wiki page) and suddenly everyone gets it. Someone once did a study where they gave the task to, I think 6-year olds, using stuffed toys instead of cards, and in a context with a nice story around it, and they almost all got it right.
I've seen kids who were supposed to solve problems like 5 ?? 2 x 3 where the ?? needs to be filled with the symbol for greater, equals or less-than. Quite apart from getting the symbol the wrong way round ("the crocodile's mouth opens towards the larger number"), they'd think something like "well 5 is bigger than 2, and 5 is bigger than 3, so it's 5". But ask them whether they'd rather have a stack of five $1 bills (or coins) or two stacks of 3, and suddenly they not only pick the right answer but can even explain "well if you have two stacks of 3, you put them on top of each other you have 6, so that's like the 5 and then you have one left over".
Also, everyone ever who runs away screaming at "x + 2 = 5" because the x summons demons or something, but "[ ] + 2 = 5, what goes in the box?" they can do without a problem.
So yes, kids need to count pebbles, blocks of wood (Cuisenaire rods! ❤), and other things that they can not only visualise, but also manipulate with their hands and feel them as physical objects as they're moving them around or counting them - that's where the somatic part comes in. Before you learn to count, you learn to count objects. And then you learn to do it on the abacus, still moving beads around and still using your hands, but the beads now have superpowers.
I've recently been reading H. Wu's "Basic Skills versus Conceptual Understanding" (https://bioscience.tripod.com/readings/basicskillvsconcpt.pdf) which I like in many ways - it defends teaching longhand addition, digit by digit and carry the ones, not only because that means you can use it to solve subproblems in more interesting questions later on, but also because the whole thing actually makes sense and you can teach it that way. Wu's suggestion is, I think, the philosophic to the abacus' somatic - an explanation of the algorithm in terms of properties of addition like that a+b is the same as b+a or that you can do a+b+c+... in any order you like, which is one of the things that makes both the abacus and the algorithm work. But I'd personally teach the abacus first, and then when you do the paper version someone or other will go "It's just like the abacus! But on paper!"
About the tenth bead - I think it's supposed to be to carry 1, so you can add numbers and then adjust at the end to make say 2,10,4 become 304. Or to do the "borrow" thingy when you're subtracting. I would make the tenth bead a different color! (EDIT: https://journals.sagepub.com/doi/full/10.1177/10323732221132005 - yes, it's a "carry one" thing. The idea is that for 8+3, you set 8 beads on the units, then slide 3 over one by one, if you run out of beads because all 10 are over already, you reset the row, add one on the tens, and move on. If you end up with all 10 over at the end of the sum, you have to adjust upwards.)
But you can also shift the carry over immediately when you need to. Otherwise you get stuck when you have to carry more than one, when you're multiplying. There is another argument for extra beads in some cases, like on the Chinese suanpan: https://web.archive.org/web/20110927085436/http://webhome.idirect.com/~totton/suanpan/ but you can also work with other methods just fine that don't need the extra beads. If you're trying to get kids to learn place value in the decimal system, as you said, you need 9 beads. Not more, and not less.