
1. A problem
Arithmetic is a pain: our brains weren’t designed to work with numbers higher than about a half dozen.
We in the modern West, of course, have developed ways to solve this — pencil and paper algorithms, calculators, and so on. The trouble is that these rob us of the chance to actually understand the math. Doing equations on paper is cumbersome, and a distraction; doing them on a calculator entirely hides what’s going on.
2. Basic plan
Teach kids how to use the Japanese soroban — a specialized abacus created to be actually used — and then actually use it in place of a calculator.
3. What you might see
Kids flicking beads around with laser focus. Eventually, students flicking their fingers without a soroban present, working through hard arithmetic problems in their heads.
4. Why?
We’ll discuss this later in FREAKY FEATS OF MENTAL MATH°, but one of the grand purposes of teaching math is to enter into a quantified understanding of the world. This is the territory of modern science, in which “thinking” begins to look more and more like “computing”.
5. Egan’s insight
Where do we see this in the human experience?
No abacus, no civilization. To run a complex society, you need to give ordinary people the ability to compute big numbers — and before the spread of Arabic numerals, physical abacuses were the best game in town. (The Romans even invented an abacus to add and subtract Roman numerals, which I find simultaneously breath-taking and horrifying.)
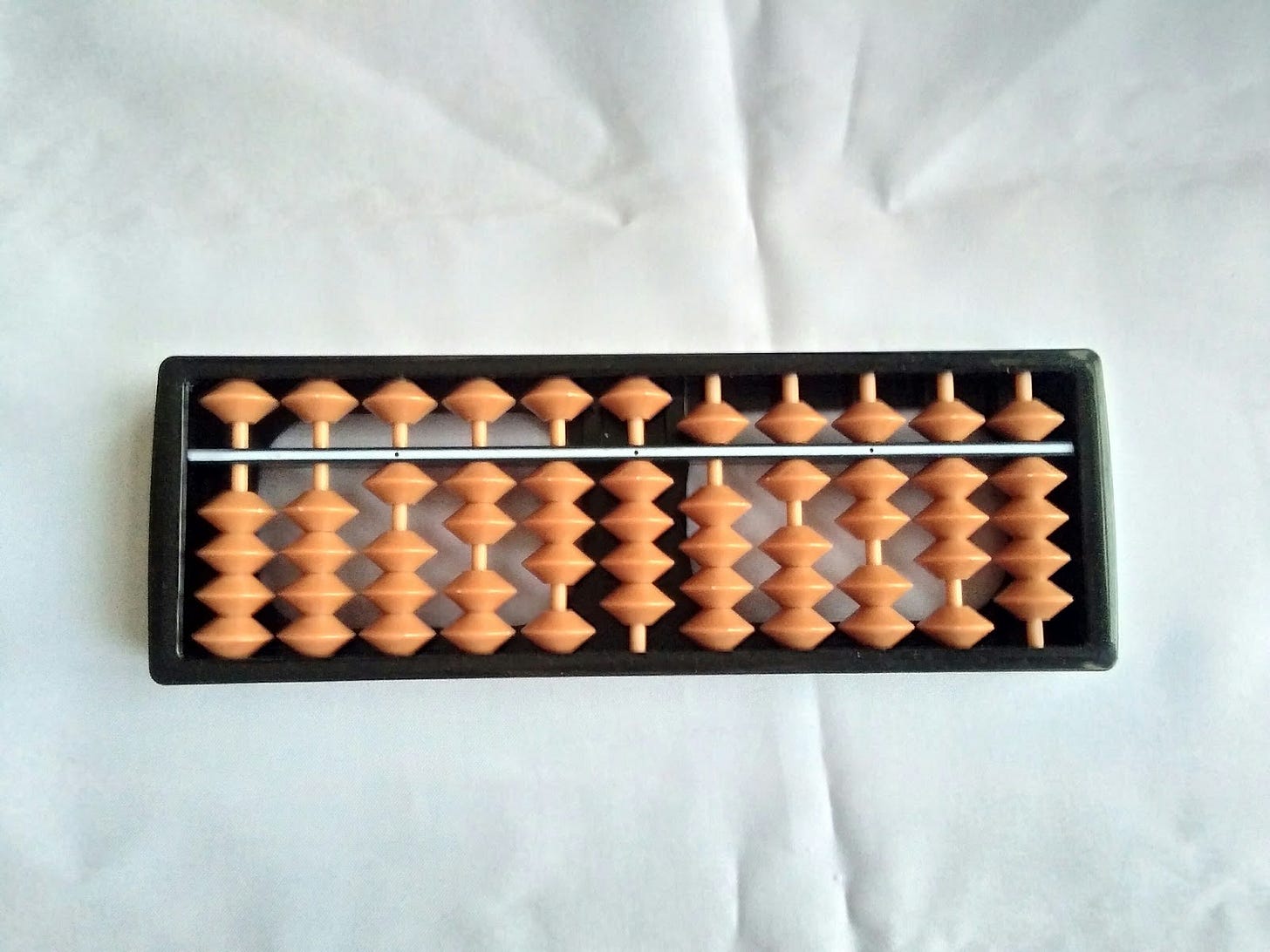
The Japanese soroban itself spent a long time in development. Its predecessor was the ancient Chinese suanpan, which dates back to the second century BC. It got a major makeover, however, in the mid-1800s, when the two top beads (called the “heavenly beads”, as opposed to the five “earth beads” at the bottom) were reduced to one.
How might this build different kinds of understanding?
In BASIC ABACUS° I suggested that an abacus sits in the Goldilocks Zone between SOMATIC (🤸♀️) and PHILOSOPHIC (👩🔬) understanding: not too abstract, not too concrete. A soroban pulls the same trick — using beads as 🧙♂️METAPHOR to stand in for, well, literally anything. (What do these weird emoji mean?)
6. This might be especially useful for…
Kids who’d enjoy problem-solving, if only they didn’t get bogged down in the arithmetic.
7. Critical questions
Q: Isn’t this outdated?
As a tool that adults use — maybe?
One hears that these are still in use in business around Asia. One also hears that an ancient sauropod prowls the jungles of Congo. For both I say pics or it didn’t happen. I wouldn’t be surprised if the temptations of getting the correct answer immediately has pushed the soroban to the side for virtually all adults, at least the non-eccentric.
But the point isn’t to be a replacement for the calculator. The real purpose is to connect the fundamental moves of arithmetic with your body, so mid-level math becomes easy, and easy math becomes automatic.
Do you have any experience in using a soroban, or in being part of a school system that taught it? Frankly, WE WOULD LIKE TO KNOW ABOUT IT. Become a subscriber and join in the comments conversation.
8. Physical space
Buy one! They’re oh-so-cheap. (If anyone has opinions on what high-quality ones are, please share ‘em.)
9. Who else is doing this?
As noted, many schools in Japan. And quite a lot of private tutors around the world, including in the States.
How might we start small, now?
What number is this? (Remember: flicking up an “earthly bead” means 1, flicking up a “heavenly bead” means 5.)
10. Related patterns
This is a high rung on a ladder. When kids are you, start with a BASIC ABACUS° to help them see the deep patterns of base-10 math. Then help them internalize arithmetic with FINGER MATH°, which uses each finger as a bead and the thumb as a special “five” bead… which perfectly parallels the soroban’s “heavenly bead”. So bring this pattern in next, and teach them to quickly calculate even big numbers.
Then, extend that to helping kids to FREAKY FEATS OF MENTAL MATH°. And from there, the world opens up.
Because now we get into science territory. Possessing an easy facility with numbers, kids can make skilled GUESSTIMATES° of things in the natural world and start GETTING COMFY WITH BIG NUMBERS°. Eventually they can become MASTERS OF MEASUREMENT°… which will allow them to make FERMI ESTIMATES° as naturally as the rest of us blow our noses.
Math is the deep foundation of PHILOSOPHIC understanding. And repairing the structural weaknesses in most people’s number sense seems one of the surest ways to help people get there.
Afterword:
Thanks to everyone who’s been nominating patterns for me to write next! Gears are moving. Feel free to suggest more in the comments.
Last week’s livestream went wonderfully — I think we’ve hit our stride, and Eganized the history of the tax code (you can watch it here). This Thursday (9pm Eastern / 6pm Pacific) we’ll be picking a boring topic from math, and using ChatGPT to make it meaningful. Join us, and invite a friend!









"The real purpose is to connect the fundamental moves of arithmetic with your body, so mid-level math becomes easy, and easy math becomes automatic."
These are the insights at the heart of Papert & Solomon's writings on LOGO and runs through Papert's larger works (Mindstorms, The Children's Machine)
I brought abacii into my CS classroom last week as a concrete example of a format / syntax. I've picked it up a half dozen more times since that first lesson because, once the semantic concept of the abacii is accessible in student's heads, it's a really convenient simile target for many cs concepts. Pass by Value/Reference / Object is a fun demonstration if you have a visually distinct set of abacii!